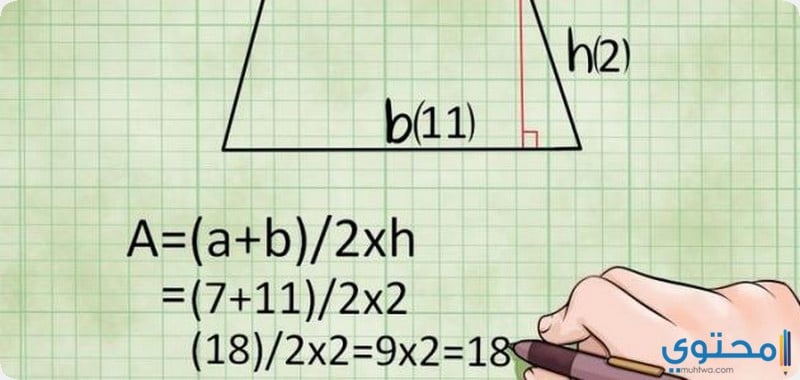مساحة شبه المنحرف بالطرق المختلفة
مساحة شبه المنحرف بالطرق المختلفة عبر موقع محتوى, شبه المنحرف من الأشكال الهندسية الأساسية ، التي لها طرق مختلفة من الاستخدام في النظريات الهندسية والعملية والفيزيائية، وانطلاقا من هذا الأمر ، اليكم كيفية حساب مساحة شبه المنحرف.
شبه المنحرف
هو أحد الأشكال الهندسية الرئيسية، ويتكون من ضلعان متقابلان متوازيان على الاقل ،حيث أنه شكل رباعي الاضلاع، يكون فيه ضلعين فقط متوازيين بينما يعتبر متوازي الاضلاع، شكل مستنثنى تماما من شكل شبه المنحرف، حيث يتضمن شبه المنحرف الضلعين المتوازيين، ولكنهم غير متساويين، فيكون الضلع الاكبر فيهما يمثل القاعدة الكبرى، و الاصغر القاعدة الصغرى.
حساب مساحة شبه المنحرف
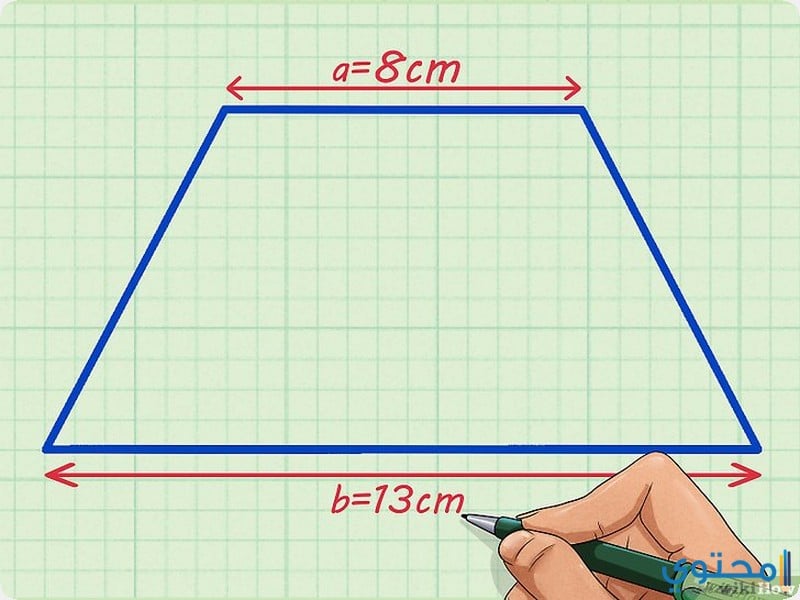
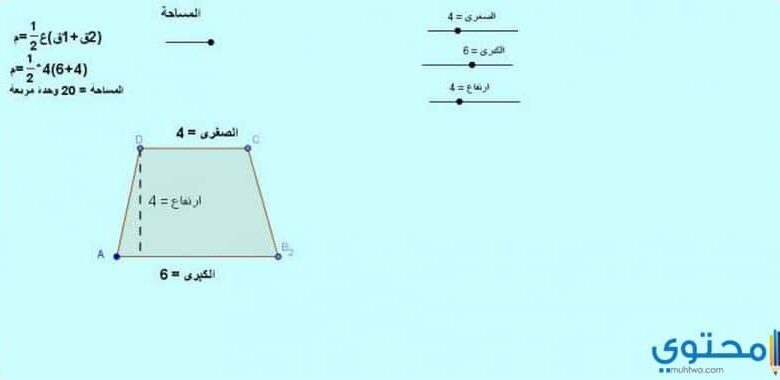
تحسب مساحة شبه المنحرف بأكثر من معادلة رياضية وطريقة حسابية، ما بين القاعدة الأولى التي تقول بأن مساحة شبه المنحرف = (طول القاعدة الكبرى + طول القاعدة الصغرى )\2 ) × الارتفاع.
أي أن مساحة شبه المنحرف = ( مجموع القاعدتين \ 2 ) × الارتفاع، جدير بالذكر أن الارتفاع في شبه المنحرف لقائم الزاوية ضلع من اضلاع شبه المنحرف عمودي على القاعدة الكبرى، اما في انواع شبه المنحرف الاخرى فهو المسافة العمودية بين القاعديتن المتوازيتين.
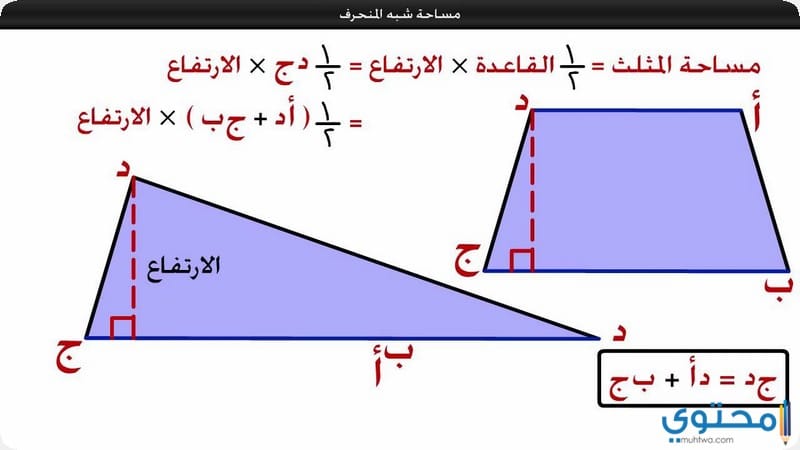
أما الطريقة الثانية لحساب مساحة شبه المنحرف تكون عن طريق تقسيم شبه المنحرف الى اشكال مثل مستطيل و مثلث او مربع و مثلث او متوازي اضلاع و مثلث، أيا كان الشكل الهندسي.
ولكن المراد أن يتم التقسيم لشكل هندسي يسهل حساب مساحته، ومن ثم حساب كل شكل هندسي وحده، مثل يمكن تقسيم شبه المنحرف الى ثلاث اشكال مثلثين ومستطيل بحيث يكون مساحة شبه المنحرف، مساحة المثلث الاول + مساحة المثلث الثاني + مساحة المستطيل.
انواع شبه المنحرف
- أولا شبه منحرف عام ، وهو شبه المنحرف وهو مضلع رباعي، وله ضلعان متوازيان و له قطران غير متساويان يتقابلان في نقطة ما ، ومن هنا يكون الارتفاع المسافة العمودية بين الضلعين المتوازيين، وبالتالي فان هذا النوع من شبه المنحرف يتكون من اربع زوايا غير متساوية مجموع قياسها 360 درجة كما ان زاويتان محصورتان بين الضلعين المتوازيين مجموعهما يساوي 180 درجة.
- ثانيا شبه منحرف متساوي الساقين ، حيث يكون فيه ضلعان متقابلان متوازيان و الضلعين الآخرين متقابلان و متساويان في الطول و غير متوازيين ، أما طول قطريه فهو متساوي .
- ثالثا شبه منحرف مختلف الاضلاع ، وهو يتكون من اربع اضلاع اثنان متوازيان غير متساويان وهما يمثلان قاعدتي شبه المنحرف ، و اثنان غير متوازيين و غير متساويين و له قطران غير متساويان يتقاطعان في نقطة ما .
- رابعا شبه منحرف قائم الزاوية، حيث يضم زاويتين قائمتين ،و الارتفاع في هذه النوع من شبه المنحرف، يمثل الضلع العمودي على القاعدة الكبرى، وهو بالطبع أحد أهم اضلاع شبه المنحرف و يمثل الارتفاع لشبه المنحرف .
قدمنا لكم عبر موقع محتوى المزيد حول مساحة شبه المنحرف، بالطرق الحسابية المختلفة، فضلا عن توضيح أهم أنواع أشكال شبه المنحرف الموجود في علوم الرياضيات والهندسة.