بحث عن الاتصال والنهايات كامل
علوم الرياضيات سوف تلاحظ وجود التكامل الذي يعين على إعداد المزيد من الوظائف المختلفة، التي تؤثر بشكل أو بأخر على الحجم والمساحة والعديد من المفاهيم الأخرى، تنشأ كافة تلك الأمور عن طريق جمع البيانات الغير محدود، يُعتبر التكامل هو إحدى العمليات الرئيسية لحساب كلا ًمن التفاضل والتكامل بالإضافة إلى التمايز.
بحث عن الاتصال والنهايات
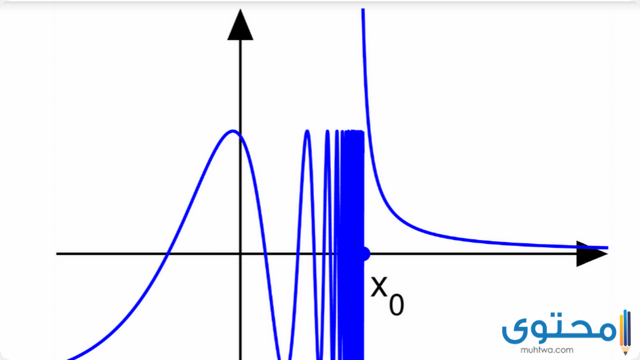
عندما تكون القيمة “س” قريبة من القيمة “ج” ولكنها لا تساويها، فإن الاقتران يساوي تقريباً “ك”، كما أن مفهوم س ¬ جـ، يعني أن قيمة “س” أقل قليلاً من قيمة “ج”، أو من الممكن أن تكون أكبر قليلاً من قيمة “ج”، ولكن في النهاية هي لا تساوي “ج”.
- تُعد النهايات هي من إحدى مبادئ التفاضل، لأنها تهتم بدراسة الاشتقاق عن طريق بعض المعلومات والمفاهيم المختلفة الخاصة بالكميات متناهية الصغر.
- بني التفاضل على النهايات بهدف دراسة اشتقاق الدالة، بتلك الطريقة يُمكننا أن نعلم بأن مفهوم النهايات مرتبط بشكل وثيق بمفهوم الاشتقاق، والعكس هنا صحيح.
- مفهوم الاشتقاق مرتبط بشكل قوي بالتغييرات التي من الممكن أن تظهر على الدالة، على سبيل المثال: x = 1 عندما y = 2، أي في تلك الحال x لن تكون 1 إلا في حالة أن تكون y = 2 كتعويض في إحدى الدوال.
- يُعتبر حساب التفاضل والتكامل من الأمور التي تحدث في العديد من الحسابات المختلفة، أي يُمكنك من خلالها دراسة بعض التغيرات المستمرة، بعدة طرق مختلفة أو بنفس الطريقة، لأن الجبر والهندسة لهم فرعين وهما: التفاضل والتكامل.
- التكامل يختص بالمعادلات الفورية وبعض المنحدرات والمنحنيات أيضًا، أما التفاضل فيختص بالمساحات التي تقع على المنحنيات، وهنا فرعان فيما بينهم يتم من خلالهم التسلسل إلى نهاية السلسلة.
استطاع إسحاق نيوتن أن يقوم بتطوير المزيد من العلوم المختلفة، ومنها علم التفاضل والتكامل، يتم استخدامه على نطاق واسع في بعض العلوم، منها علوم الهندسة والاقتصاد، إذا قمت بالحصول على دورة جيدة في التفاضل والتكامل من الممكن أن تكون باب لك، لكى تتمكن من الدخول في عدة دورات أخرى وعدة علوم مختلفة.
شاهد أيضًا: بحث عن المخدرات وأضرارها مع المراجع والعناصر
حساب التفاضل والتكامل سابقا
استكمالاً لحديثنا حول الاتصال والنهايات، في السابق أي منذ الأسرة الثالثة عشر تقريباً، كان هناك الكثير من الأفكار المختلفة التي ساعدت في الحصول على تطور رهيب في علوم الرياضيات خاصة في التفاضل والتكامل.
- كانوا يقومون باستخدام ورق البردي من أجل معرفة المزيد من الطرق والتجارب للحصول على نتائج سريعة، قاموا باستخدام بعض الصيغ البسيطة وبعض الإشارات التي تهدف إلى وصول المعنى.
- كان هناك عصر خاص بالرياضيات اليونانية وتم استخدامه في التطوير من الرياضيات، كان هذا العصر بتاريخ 355 قبل الميلاد، واستطاع أيضًا أرخميدس أن يقوم بالتطوير بشكل أكبر في جزئية التفاضل والتكامل.
- تم اختراع الاستدلال الذي كان يشبه كثيرا التفاضل والتكامل، وتم اكتشاف طريقة الاشتقاق فيما بعد بعدة سنوات، تم اكتشافها لأول مرة في دولة الصين، وقام كلاً من أسس زوج نجزي ، ابن زو تشونغ تشي بالعثور على معرفة حجم الكرة.
شاهد أيضًا: استراتيجية فراير في الرياضيات
التفاضل والتكامل في القرون الوسطى
وفي سياق الحديث حول بحث عن الاتصال والنهايات استطاع حسن بن الهيثم أن يتمكن في الحصول على نتائج مثالية في علم الرياضيات، هذا بعد كفاح طويل قد استمر إلى سنوات عدة، حيث استطاع أن يقوم بتغيير صيغة المجموعة الرابعة في التفاضل والتكامل.
- سمحت له تلك الصيغة بأن يتمكن من معرفة المربعات المتكاملة، بالإضافة إلى القوة الرابعة بحسب حجم القطع المكافئ لتلك الاستنتاج، شعر بالكثير من الإرهاق ولكنه استطاع أن يبرز نفسه ويترك وراءه أثر كبير.
- أما في القرن الرابع عشر، قدموا الكثير من العلماء الهنود بالرياضيات طرق تشبه طريقة التمايز، وهي التي تنطبق بشكل كبير على الدوال المثلثية، أصبحت النظرية كاملة يعرفها كافة علماء الرياضيات.
- على الرغم من جميع تلك النتائج التي استطاعوا أن يتوصلوا إليها في وقت قليل، إلا أنهم لم يتمكنوا من أن يحصلوا على أفكار خاصة تجمع بين كلاً من المشتق والتكامل.
- التعرف على العلاقة فيما بينهم، أو معرفة طريقة ما لتحويل حساب التفاضل والتكامل، إلى أداة جيدة لكي تحل لهم العديد من المشاكل التي تواجهنا اليوم.
بحث عن الاتصال والنهايات كامل يوضح لك ما لم تكن على علم به من قبل، لأن علوم الرياضيات من أكثر العلوم الشيقة التي يُمكنك أن تتعرف عليها أكثر بدافع الثقافة أو الدراسة، وتعمل على توسيع مداركك وطريقة فهمك بشكل مثالي.
