وجه الاختلاف بين المربع والمعين والفرق بينهم
تحتوي مادة الهندسة على عدة مفاهيم وأشكال مختلفة أهمها على الإطلاق الأشكال الرباعية مثل (المربع، المستطيل، المعين، متوازي الأضلاع)، وتم تسميتها بهذا الاسم لأنها تتكون من أربعة أضلاع، وبالتالي تتكون من أربع زوايا، وعلى الرغم من كونها أشكال رباعية إلا أنها تختلف في بعض الخصائص التي تميز كل شكل عن الآخر.
وجه الاختلاف بين المربع والمعين
يخلط العديد من الطلاب بين المربع والمعين، نظراً لأن شكل كل منهما متقارب من حيث الطول والشكل وأيضا الخواص.
بالرغم من المعين والمربع من عائلة المضلع الرباعي إلا أنهما يختلفان عن بعضهما البعض في التعريف وقياس الزوايا وغيرها، لذا دعونا نلقي نظرة على وجه الاختلاف بين المربع والمعين.
تعريف المعين
- المعين هو أحد الأشكال الهندسية الرباعية.
- ويمكن تعريفه بأنه مضلع رباعي الشكل، وجميع أضلاعه متطابقة.
- وكل ضلعين” غير متجاورين” أي متقابلين في المعين متوازيين.
- وكل زاويتين متقابلتين من الزوايا متساويتين في القياس.
شاهد أيضًا: ما هو الفرق بين المربع والمعين والمستطيل
اشكال المعين
- يمكن تعريف أشكال المعين على أنه عبارة عن مثلثين ولكن متساويين الساقين.
- بالإضافة إلى هذان المثلثان يشتركان مع بعضهما البعض في قاعدة المثلث، مع حذف قاعدة المثلث الأخرى.
- أي أنه شكل رباعي أو متوازي أضلاع فيه كل ضلعين متقابلين متوازيين.
- وكل ضلعين متجاورين متساويين.
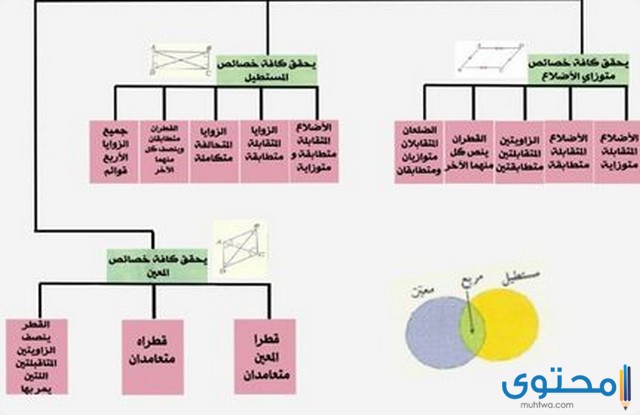
خواص المعين
يحتوي المعين على العديد من الخواص التي تميزه عن الأشكال الرباعية الأخرى، حيث يضم بشكل كبير خواص متوازي الأضلاع، ومن أهم خواصه ما يلي:
- جميع أضلاع المعين متساوية.
- كل ضلعين متقابلين من الأضلاع متوازيان.
- كل زاويتين متقابلتين من الزوايا متساويتان.
- قطراه متعامدان وينصف كل منهما الآخر، وينصف أيضاً كل منهما زوايا المعين الداخلية.
- يحتوي على زاويتين حادتين وزاويتين منفرجتين.
- إذا كانت إحدى الزوايا قائمة، فإنه يصبح مربع وليس معيناً.
- يعتبر قطراه محاور تناظرية، كما أن نقطة تقاطع هما هي نقطة التناظر.
- ويعد شكلاً رباعياً مماسياً، لأن كل ضلع من أضلاعه يعتبر مماساً لدائرة واحدة فقط.
مجموع زوايا المعين
- مجموع زوايا المعين هو 350 درجة، ويحتوي على أربع زوايا.
- كل زاويتين متقابلتين متساويتين.
- ويحتوي على زاويتين منفرجتين وأخرى حادتين، أي أن زواياه ليست متساوية في القياس.
- وإذا تساوت الزوايا في القياس أصبح الشكل الرباعي المعين “مربع”.
شاهد أيضًا: تعرف علي قانون محيط المربع ومساحته
مساحة المعين
- هي المساحة الفارغة الموجودة داخل حدود الأضلاع الأربعة له.
- ويمكن حساب المساحة من خلال ثلاثة طرق وهم:
دلالة الارتفاع وطول أحد الأضلاع
- مساحة المعين = طول الضلع× الارتفاع.
- أي أن (م=ل× ع)، أي أن الرمز(م) تعني مساحة المعين.
- والرمز (ل) يعني طول أي ضلع من أضلاعه المتساوية، والرمز (ع) هو الارتفاع.
- والارتفاع (ع) هو القطعة المستقيم العمودية التي تصل بين الضلعين المتقابلين في المعين.
حساب المساحة بدلالة طول القطرين
يمكن حساب مساحة المعين من خلال طول القطريين باستخدام القانون التالي:
- حساب مساحة المعين= (القطر الأول × القطر الثاني) ÷2.
- باستخدام الرموز م = ق× ل÷2
حساب المساحة بدلالة طول الضلع
يمكننا إيجاد مساحة المعين إذا وجد لدينا طول أحد أضلاع المعين، وأيضاً قياس إحدى زواياه معلومين، من خلال القانون التالي:
- مساحة المعين= مربع طول أحد أضلاع المعين× جيب إحدى زواياه.
- ويعبر عنه بالرموز: م= (ل)²×جا(α).
تعريف المربع
- هو أحد الأشكال الهندسية الرباعية.
- ويمكن تعريفه بأنه مضلع رباعي الشكل، أو شكل هندسي رباعي مغلق، جميع أضلاعه متساوية في الطول.
- وكل ضلع من أضلاع المربع متعامد على الآخر، كي يشكل زاوية قائمة.
- جميع الزوايا متساوية، وتمثل كل زاوية من زوايا المربع 90 درجة.
شاهد أيضًا: أنواع المثلثات حسب الاضلاع حسب الزوايا
قوانين المربع
توجد مجموعة من قوانين المربع، يمكن من خلالها معرفة المساحة والمحيط، ويمكن تلخيص هذه القوانين في التالي:
القانون الأول
- ينص القانون الأول على أن مساحة المربع يمكن حسابها من خلال مساحة المستطيل.
- خاصةً وأن مساحة المستطيل بها خصائص تتطابق مع المربع.
- أي أن مساحة المربع = الطول × العرض أي طول الضلع × نفسه.
القانون الثاني
- مساحة المربع يعتمد على معرفة القطر.
- = (مربع طول القطر /2)، ويمكن إيجاد المساحة من خلال حساب طول القطر.
القانون الثالث
- حساب مساحة المربع من خلال حساب الأضلاع الأربعة له.
- أو ما يعرف بمحيط المربع، حيث يساوي محيط المربع (طول الضلع الأول + الثاني+ الثالث + الرابع).
- أو بصيغة أخرى أن محيط المربع = طول الضلع×4.
القانون الرابع
- يعتمد القانون الرابع في حساب مساحة المربع على حساب قطر المربع.
- عن طريق العديد من العمليات الحسابية المختلفة.
خصائص المربع
وفي السياق الحديث حول المربع والمعين، المربع أحد الأشكال الهندسية الرباعية التي تتميز عن غيرها من الأشكال والمضلعات بالعديد من الخصائص وهي كالتالي:

- يتكون المربع من أربعة أضلاع، وأربعة رؤوس، وأربعة أحرف، وأيضاً أربعة زوايا داخلية.
- كل زاوية من الزوايا قياسها هو 90 درجة، ومجموع قياسات زواياه هو 360 درجة.
- جميع الأضلاع متساوية في الطول.
- كما يعد أحد أنواع متوازي الاضلاع، لأن كل ضلعين متقابلين متوازيين ومتساويين في الطول.
- بالإضافة إلى أن كل زاويتين متقابلتين من الزوايا متطابقتين متساويتين في القياس.
- يحتوي المربع على قطران اثنين فقط، يتعامد كل منهما على الآخر، وينصف كل منهما الآخر إلى جزأين متساويتين.
- ينصف القطران الزوايا إلى زاويتين متساويتين في القياس، قياس كل منهما هو 45 درجة.
- يضم أربعة محاور، تسمى محاور التناظر، اثنين منهما هما قطرا المربع.
- والاثنين الآخرين هما القطعتين المستقيمتين الواصلتين بين منتصف كل ضلعين متقابلين من أضلاع المربع، وتنصف كل منهما الآخر.
- نقطة تقاطع القطران في المربع هي بمثابة نقطة التناظر له.
- ومن خصائصه أيضاً والتي تميزه عن غيره من الأشكال الرباعية بأنه مسطح، لذلك فهو ذو أبعاد ثنائية.
شاهد أيضًا: كم تبلغ مساحة قطر بالكيلو متر المربع
مساحة المربع
- يعتبر المربع أحد الأشكال الرباعية الهامة والمميزة، خاصة في مفهوم الأشكال الهندسية بشكل عام.
- لأنه بني على أساسه تعريف المساحة لكافة الأشكال والوحدات المربعة.
- ويمكن معرفة مساحة المربع من خلال القاعدة التالية:
- مساحة المربع = طول الضلع × طول الضلع.
- أو طول الضلع × نفسه.
- أو يمكن القول تربيع الضلع.
- مثال: لوحة مربعة الشكل، طول ضلعه يساوي ٤سم، أوجد مساحة اللوحة.
- مساحة اللوحة =4×4= 16 سم مربع.
محيط المربع
- يمكن معرفة محيط المربع من خلال جمع مجموع أطوال أضلاع، وذلك بداية من الضلع الأول وصولاَ للضلع الرابع.
- كما يمكن القول إن محيط المربع يساوي مجموع أطوال أضلاعه.
- أو محيط المربع =طول الضلع × نفسه.
- مثال: لوحة مربعة الشكل، طول ضلعه يساوي 50 سم، أوجد محيط اللوحة؟
- محيط اللوحة =4×50= 200 سم.
عدد أقطار المربع
- يمكن معرفة عدد أقطار أي مضلع أو شكل هندسي من خلال قانون خاص يوضح عدد أقطار أي مضلع.
- حيث يتكون المضلع سواء مضلع ثلاثي أو رباعي أو خماسي أو غيره من عدد من أضلاع.
- قانون أقطار المضلع =ن (ن-3) /2، حيث يمثل الرمز (ن) عدد أضلاع المضلع.
- أقطار المربع =ن(ن-3) /2 =4× (4-3) /2
- إذن عدد أقطار المربع هما قطران فقط.
بعد أن تعرفنا على وجه الاختلاف بين المربع والمعين وجدنا عدة اختلافات منها الخصائص، المساحة، المحيط ونتمنى أن نكون قد وفقنا في شرح كافة التفاصيل بينهما، ويسعدنا تلقي أي استفسارات حول قوانين مادة الرياضيات المختلفة.
