بحث عن البرهان الجبري رياضيات أول ثانوي

تعد الرياضيات من العلوم الأساسية التي تسهم في تطوير مهارات التفكير والتحليل والاستنتاج، ومن بين مفاهيم الرياضيات المهمة التي تدرس في المرحلة الثانوية هو “البرهان الجبري”، ويتميز بأهمية كبيرة لكونه يركز على إيضاح الأفكار الرياضية بدقة، ويعتمد على استخدام القوانين و الخواص الجبرية للتحقق من صحة العبارات الرياضية.
مقدمة بحث عن البرهان الجبري
- البرهان الجبري هو طريقة تستخدم للتحقق من صحة العبارات أو النظريات الرياضية عن طريق تطبيق قواعد جبرية وخطوات منطقية واضحة.
- يتميز البرهان الجبري بأنه يعتمد على التسلسل المنطقي للأفكار، مما يعزز من صحة الحلول ويقلل من الأخطاء في العمليات الحسابية.
- تكمن أهمية البرهان الجبري في كونه يساعد الطلاب على تطوير مهارات التفكير النقدي والتحليل، ويعزز من قدرتهم على حل المشكلات الرياضية بطريقة منهجية ومدروسة.
- تتجلى أهمية البرهان الجبري في أنه يتيح للطلاب فهم أسس العمليات الحسابية والقواعد الجبرية بعمق، مما يسهم في تحسين مهاراتهم الرياضية وتطوير قدراتهم على التفكير المنطقي.
تاريخ البراهين
يعود تاريخ البراهين الرياضية إلى آلاف السنين، حيث كانت واحدة من أهم وسائل تحقيق المعرفة والتحقق من صحة النظريات الرياضية، وتطورت أساليبها عبر العصور، واختلفت طرق استخدامها من حضارة إلى أخرى، فساهمت في إثراء الفكر الرياضي وتطويره ليصل إلى صورته الحديثة.
البراهين في الحضارات القديمة:
- في الحضارة المصرية القديمة استخدم المصريون القدماء مبادئ الرياضيات مثل الهندسة، في تنظيم حياتهم اليومية خاصة في مجالات الهندسة المعمارية والزراعة.
- لم يُعتمد في هذه الحضارة على البرهان بمعناه المعاصر، بل كان يعتمد على أساليب عملية وتجريبية لتطوير الحلول الهندسية.
- في الحضارة البابلية اهتم البابليون بالرياضيات خاصة في الجبر والحسابات الفلكية، ووضعوا أسساً لتطوير العمليات الحسابية.
- رغم ذلك لم يعتمدوا على مفهوم البرهان الرياضي المبني على القواعد المنطقية، بل اعتمدوا على الجداول والقيم العددية.
الإغريق وتأسيس البرهان الرياضي:
تعتبر الحضارة الإغريقية أساس تطوير البرهان الرياضي بمعناه الدقيق، وقد أسهم الإغريق في صياغة قواعد البرهان وتنظيمها لتصبح جزءًا لا يتجزأ من الرياضيات، ومن أشهر العلماء الذين ساهموا في هذا المجال هو إقليدس، الذي يُعتبر “أبو الهندسة.”
- في حوالي القرن الثالث قبل الميلاد كتب إقليدس كتابه الشهير “العناصر”، الذي يُعد من أهم الكتب في تاريخ الرياضيات.
- قدم نظامًا متكاملًا من البراهين الرياضية يعتمد على المبادئ والبديهيات، وهو أول من وضع الأسس لمنهج الاستدلال المنطقي.
- يعتبر عمله هذا حجر الزاوية في تطوير الرياضيات الحديثة.
- أسهم فيثاغورس وأتباعه في تطوير قواعد هندسية، ومن أهم البراهين التي قدمها كانت “مبرهنة فيثاغورس” التي تُعد مثالًا على البرهان الجبري والهندسي.
- ساهم أرخميدس في استخدام البراهين لاستنتاج قوانين في الهندسة وحساب المساحات والحجوم.
- يُعتبر من أوائل العلماء الذين استخدموا البرهان عن طريق الاستقراء، خاصة في حسابات الأشكال المتعرجة والأسطوانات.
التطور في العصور الوسطى:
- في العصر الذهبي للحضارة الإسلامية حقق العلماء المسلمون إنجازات كبيرة في تطوير الرياضيات، خاصة في مجال الجبر والهندسة.
- طور العلماء مثل الخوارزمي وكتاباته في “الكتاب المختصر في حساب الجبر والمقابلة” مفاهيم البرهان الرياضي.
- حيث استخدموا براهين منظمة لحل المعادلات الجبرية وتطوير مبادئ الرياضيات.
- في العصور الوسطى بدأت الجامعات الأوروبية بتدريس الفلسفة والرياضيات على طريقة الإغريق، حيث اعتمدوا على براهين إقليدس كأساس للتدريس.
- كانت أغلب البراهين في هذه الفترة تعتمد على الهندسة وعلم الفلك.
النهضة الأوروبية والتوسع في أساليب البرهان
في فترة النهضة الأوروبية، ومع ازدهار العلوم والفلسفة توسعت أساليب البرهان، وشملت الجبر والتحليل الرياضي، وبدأ العلماء في تبني منهجيات جديدة للتفكير الرياضي، وظهرت براهين تستخدم الجبر التحليلي وحساب التفاضل والتكامل.
- أسهم الفيلسوف والرياضي الفرنسي رينيه ديكارت في تطوير الهندسة التحليلية، وربط بين الجبر والهندسة من خلال تقديم فكرة نظام الإحداثيات الديكارتية، ما سمح بتطبيق البرهان الجبري على مسائل هندسية.
- يعتبر إسحاق نيوتن وغوتفريد فيلهلم لايبنيتز من أهم العلماء الذين طوروا حساب التفاضل والتكامل في القرن السابع عشر، وقدموا براهين رياضية جديدة تعتمد على التحليل.
تطور البراهين في العصر الحديث
مع بداية القرن التاسع عشر، تطورت أساليب البرهان بشكل ملحوظ، حيث ظهرت مجالات رياضية جديدة مثل الجبر المجرد ونظرية المجموعات، وتوسع ليشمل براهين على المستوى المتقدم في التحليل الرياضي، والجبر، والهندسة الجبرية.
- نظرية المجموعات: أسهم جورج كانتور في وضع أسس نظرية المجموعات التي غيرت شكل البرهان الرياضي وجعلته أكثر شمولية، وأدخلت مفاهيم جديدة مثل المالانهاية والتعداد.
- البرهان بالطريقة الاستنتاجية والبديهية: تطورت منهجيات البرهان مع استخدام المنطق الرمزي الذي أسسه علماء مثل جوتلوب فريجه، وظهور النظرية الشكلية على يد ديفيد هلبرت، مما جعل البرهان الجبري أكثر تنظيماً ووضوحاً من الناحية المنطقية.
أنواع البرهان الجبري
- البرهان المباشر: يعتمد على الانطلاق من الفرضيات المعطاة للوصول إلى النتيجة المطلوبة مباشرة باستخدام القواعد الجبرية.
- البرهان غير المباشر (برهان الخلف): يعتمد على فرض عكس النتيجة التي نسعى لإثباتها، ومن ثم الوصول إلى تناقض مع الفرضيات الأصلية، مما يثبت صحة النتيجة.
- البرهان بالاستقراء الرياضي: يستخدم لإثبات صحة عبارات معينة لجميع الأعداد الطبيعية، ويتم من خلال إثبات صحة العبارة للعدد الأول ثم افتراض صحتها لعدد طبيعي معين وإثبات صحتها للعدد الذي يليه.
خواص البرهان الجبري
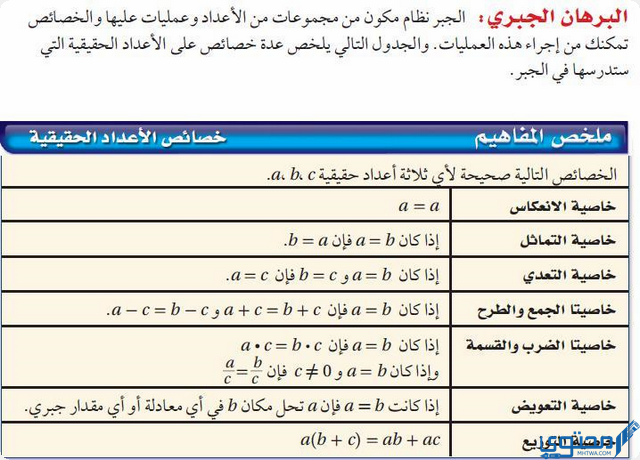
- خاصية التساوي: تنص على أن الكميتين المتساويتين تظل متساويتين بعد تطبيق نفس العملية على كليهما.
- خاصية التوزيع: تنص على توزيع عملية الضرب على عملية الجمع أو الطرح، حيث يمكن توزيع الضرب على حدود الجمع أو الطرح.
- خاصية الانعكاس: تنص على أن أي كمية تساوي نفسها، وهي أساس البديهيات الرياضية.
- خاصية الإبدال والتجميع: تسهم هذه الخاصيتان في تبسيط العمليات الجبرية وضبط خطوات البرهان.
خطوات البرهان الجبري
تعتمد خطوات البرهان الجبري على التسلسل المنطقي للأفكار، وتبدأ عادة بتحليل المعطيات المتاحة وتحديد المطلوب إثباته.
- تحديد المعطيات: وهي المعلومات التي يتم تزويدها في المسألة، وتشكل الأساس الذي ينطلق منه البرهان.
- تحديد المطلوب إثباته: وهو الهدف النهائي الذي نسعى للوصول إليه باستخدام البرهان الجبري.
- التسلسل المنطقي للحل: ويعني وضع خطوات مرتبة للوصول إلى النتيجة المطلوبة، وذلك بالاعتماد على القواعد والخواص الجبرية.
- التحقق من الحل: التأكد من صحة الخطوات ومنطقية النتائج وصولًا إلى البرهان النهائي.
اطلع على: بحث عن الوسائط المتعددة في التعليم Multimedia
تطبيقات البرهان الجبري في الحياة اليومية
يساهم البرهان الجبري في حل العديد من المشكلات العملية في الحياة اليومية، كالتخطيط المالي وإدارة المخاطر وتحليل البيانات، ويستخدم أيضًا في مجالات أخرى مثل الهندسة والفيزياء لحل معادلات تتعلق بالقوى والحركة والطاقة علاوة على ذلك يمكن أن يسهم في البرمجة وتطوير الخوارزميات.
فوائد البرهان الجبري في تنمية مهارات التفكير
إن تعلم البرهان الجبري لا يساعد فقط على تطوير المهارات الرياضية، بل يسهم أيضًا في تنمية قدرات الطلاب على التفكير المنطقي وحل المشكلات بطرق إبداعية
ويعزز القدرة على التحقق من صحة الأفكار والنظريات قبل تبنيها، ما يجعل الطالب قادرًا على التمييز بين الصواب والخطأ بناءً على أدلة منطقية ورياضية قوية.
اطلع على: بحث عن السلامة المرورية بالمقدمة والخاتمة
خاتمة بحث عن البرهان الجبري
يمثل البرهان الجبري إحدى الركائز الأساسية التي تمكن الطالب من بناء قاعدة قوية في علم الرياضيات، مما يسهم في تطوير مهاراته التحليلية والمنطقية، والقدرة على استخدام البرهان الجبري بمهارة تمثل خطوة مهمة نحو النجاح الأكاديمي والتفوق في مجالات أخرى تتطلب التفكير النقدي والتحليل.
